The Golden Jill Mining Company is interested in procuring 10,000 acres of coal mines in Powder River Basin. The mining company is considering two payment-plan options to buy the mines:
I. 100% Payment
II. Installment-Payment
The payoff received will be based on the quality of coal obtained from the mines which has been categorized as High, Normal, and Poor Quality as well as the payment plan. The profit payoff in million dollars resulting from the various combinations of options and quality are provided below:
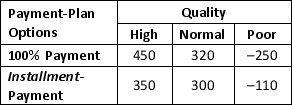a. Suppose that management believes that the probability of obtaining High Quality coal is 0.55, probability of Normal Quality Coal is 0.35, and probability of Poor Quality Coal is 0.1. Use the expected value approach to determine an optimal decision.
b. Suppose that management believes that the probability of High Quality coal is 0.25, probability of Normal Quality Coal is 0.4, and probability of Poor Quality Coal is 0.35. What is the optimal decision using the expected value approach?
Definitions:
Q3: Choosing a decision alternative that maximizes the
Q5: In a linear programming model, the _
Q10: The nurse prepares to administer an IV
Q13: A patient has been on antibiotic therapy
Q14: A patient is seen regularly for hypertension.When
Q15: Diphenhydramine (Benadryl)is an antiemetic;it is also used
Q17: A research team in at the Gonzaga
Q18: Reference - 9.1. The part-worths for each
Q31: Roger is willing to promote and sell
Q53: Reference - 11.1: Which of the following