Suppose V and W Are Finite Dimensional Vector Spaces, and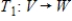

question 13

True/False

Suppose V and W are finite dimensional vector spaces, and and 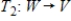are linear transformations such that 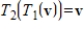for every v in V and 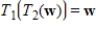for every w in W. If the matrices 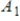, 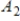represent 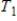, 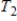respectively (with respect to the same bases for V and W), then .

---

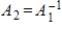Definitions:

Low Rank Positions

Low rank positions refer to jobs or roles within an organization that are at the bottom of the hierarchical structure, often involving less responsibility and requiring fewer qualifications.

Kingsley Davis

An American sociologist and demographer known for his work on population theory and the study of family structure and urbanization.

Survival of Society

The ability of a society to maintain itself and continue existing through adapting to changing conditions and challenges over time.

Ability and Talent

Natural aptitude or skill possessed by individuals, often seen as the innate potential that can be developed through practice and learning.