A 5000 ML Aliquot of a Water Sample Is Reacted with with Excess

question 3

Short Answer

A 50.00 mL aliquot of a water sample is reacted with excess potassium iodide in acidic solution to generate 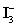.Carbon dioxide is bubbled through the solution to remove nitrogen monoxide generated.The water sample is transferred to a 500 mL volumetric flask and diluted to volume.A 50.00 mL aliquot is then titrated against 1.092 x 10⁻⁴ M thiosulfate,requiring 15.48 mL to reach the starch end point.What is the concentration in ppm? Assume solution density of 1.000 g/mL. ⇋ ⇋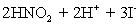

---

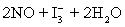
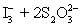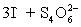
Definitions:

Producer Surplus

The difference between the amount producers are willing to accept for a good or service and the actual price they receive.

Below Equilibrium Price

A situation where the price of a good or service is set lower than the market equilibrium, often leading to a shortage.

Market Failure

A situation in which the allocation of goods and services by a free market is not efficient, often due to externalities, monopolies, or information asymmetries.

Efficient Outcome

An optimal allocation of resources where it is impossible to improve one party's position without worsening another's, often associated with maximized total welfare or utility in an economic context.