Willy's Only Source of Wealth Is His Chocolate Factory

question 33

Multiple Choice

Willy's only source of wealth is his chocolate factory. He has the utility function pc 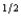_f + (1 - p) c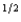
_nf, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 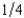. The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 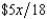whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy

• A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
• B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there was a flood or not.
• C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
• D) .enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there were no flood.
• E) enough insurance so that if there is a flood, after he collects his insurance his wealth will beof what it would be if there were no flood

---

Definitions:

Retested

The process of administering a test or assessment again to the same subject at a different time to evaluate changes, consistency, or reliability.

Regression Toward

A statistical phenomenon that suggests that extreme scores or extreme behavior are likely to be closer to the average on subsequent observations or attempts.

Illusion of Control

The overestimation of one's ability to control events or outcomes that are largely or entirely beyond their actual influence.

Standard Deviation

An indicator of the extent of variability or scatter among a collection of numbers.