Professor Kremepuff Has Published a New Textbook

question 10

Multiple Choice

Professor Kremepuff has published a new textbook. This book will be used in classes for two years, at which time it will be replaced by a new edition. The publisher charges a price of $p₁ in the first year and $p₂ in the second year. After the first year, bookstores buy back copies from students for $ 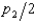and resell them to students in the second year for $p₂. (Students are indifferent between new and used copies.) The cost to a student in the first year of owning the book for a year is therefore $(p₁ - 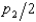) . In the first year of publication, the number of students willing to pay $v to own the book for a year is 70,000 - 1,000v. The number of students taking the course in the first year who are willing to pay at least $w to keep the book for reference rather than resell it is 70,000 - 5,000w. In the second year, the number of students who have not previously taken the course and are willing to pay at least $p for a copy of the book is 60,000 - 1,000p. If the publisher sets a price of $p₁ in the first year and $p₂ in the second year, with p₁ B3 p₂, then the total number of copies that the publisher sells over two years will be equal to

• A) 130,000 - 1,000(p₁ +).
• B) 140,000 - 1,000(p₁ -).
• C) 140,000 - 1,000p₁ - 1,000p₂.
• D) 140,000 - 3,000p₂.
• E) 130,000 - 1,500p₂.

---

Definitions:

Marginal Utility

The additional satisfaction or usefulness gained from consuming one more unit of a good or service.

Income Effect

is the change in an individual's or economy's income and how that change will impact the quantity demanded of a good or service.

Substitution Effect

The change in consumption patterns due to a change in relative prices, leading consumers to replace more expensive items with less expensive ones.

Marginal Utility Data

Information regarding the incremental benefit or satisfaction gained from consuming an additional unit of a good or service.