(See Problem 2

question 17

Multiple Choice

(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 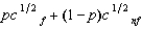, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 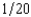. The value of Willy's factory is $300,000 if there is no flood and 0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ 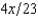whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy

• A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
• B) enough insurance so that if there is a flood after he collects his insurance, his wealth will beof what it would be if there is no flood
• C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
• D) .enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not.
• E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood

---

Definitions:

Installment Method

A tax method allowing income recognition from sales or transfers of property over time as the seller receives payments.

Deferred Payments

Payments or income that are delayed to a future date, which can have various tax implications depending on the nature of the deferral and the tax rules applicable.

Adjusted Basis

The original value of an asset adjusted for factors such as depreciation or improvements.

Like-kind Exchange

A tax deferment strategy allowing for the exchange of similar types of property without the immediate tax liability.