(See Problem 2

question 3

Multiple Choice

(See Problem 2.) Willy's only source of wealth is his chocolate factory. He has the utility function 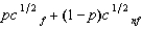, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 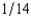. The value of Willy's factory is $400,000 if there is no flood and 0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company $ 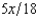whether there is a flood or not, but he gets back $x from the company if there is a flood. Willy should buy

• A) enough insurance so that if there is a flood, after he collects his insurance, his wealth will be the same whether there is a flood or not.
• B) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood.
• C) no insurance since the cost per dollar of insurance exceeds the probability of a flood.
• D) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood..
• E) enough insurance so that if there is a flood, after he collects his insurance, his wealth will beof what it would be if there is no flood

---

Definitions:

Selling Expenses

Expenses incurred directly or indirectly in making a sale, such as commissions, advertising costs, and shipping expenses.

Disallowed Loss

A loss that cannot be claimed for tax deduction purposes because it does not meet certain IRS criteria.

Capital Gains

The profit from the sale of assets or investments when the selling price exceeds the original purchase price.

Adjusted Gross Income

An individual's total gross income minus specific deductions. It's used as the basis for calculating taxable income.