Six Sigma Is One Approach for Setting Quality Expectations for a Given

question 140

Essay

Six Sigma is one approach for setting quality expectations for a given process or output. As pointed out in Chapter 17 of your text, the term "Six Sigma" comes from statistics: in a normal distribution, the area (probability) outside of +/− six (6) standard deviations from the mean value is exceedingly small. You are provided the following values from a standardized normal distribution (i.e., a distribution with a mean of zero and a standard deviation of 1.0): $\begin{array}{|c|c|}\hline \mathbf{Z} & \mathbf{p} \\\hline 0.00 & 0.50000000 \\\hline 1.00 & 0.15870000 \\\hline 1.50 & 0.06681000 \\\hline 1.75 & 0.04006000 \\\hline 2.00 & 0.02275000 \\\hline 2.50 & 0.00621000 \\\hline 3.00 & 0.00135000 \\\hline 3.50 & 0.00023270 \\\hline 4.00 & 0.00003169 \\\hline\end{array}$ Note: The Z values in the above table refer to the number of sigmas to the right of center (i.e., to the right of Z = 0). The listed probabilities, p, refer to the area to the right of the chosen Z point, as illustrated by the graph below: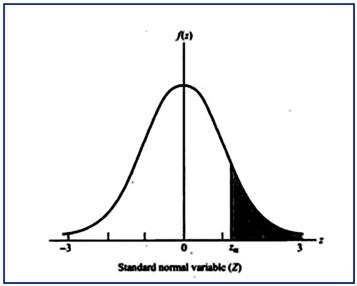 Required:
1. Given the above, what is the total probability (area under the curve) corresponding to Z = 0 +/− 1.0 sigma, rounded to two decimal places (e.g., 0.34817 = 34.82%)? How many units (out of 1,000 outputs) would have one or more defects for a process operating at one-sigma performance level? Round your answer to nearest whole number.
2. What is the total probability (area under the curve) corresponding to Z = 0 +/− 3.0 sigma, rounded to two decimal places? How many units (out of 1,000 outputs) would have one or more defects for a process operating at three-sigma performance level? Round your answer to nearest whole number.
3. Under a four-sigma control level, what is the total area in the two tails of the distribution, rounded to six (6) decimal places (e.g., 0.00004169 = 0.00417%). What is the total probability (area under the curve) corresponding to Z = 0 +/− 4.0 sigma, rounded to two decimal places? How many units (out of 100,000 outputs) would have one or more defects for a process operating at four-sigma performance level? Round your answer to nearest whole number.
4. What general conclusion can you draw based on the preceding results?

Identify key characteristics and differences between apprenticeships, internships, and other on-the-job training programs.

Understand the role and effectiveness of simulation in training programs.

Recognize the importance of behavior modeling in learning and training environments.

Distinguish between different occupations and their typical forms of training.

---

Definitions:

Trial Balance

A trial balance is a bookkeeping worksheet in which the balances of all ledgers are compiled into debit and credit account column totals that are equal.

Slide

An error in accounting that occurs when a number is incorrectly transferred from one document to another, missing or adding a digit.

Error

A mistake or discrepancy in documents or calculations, often requiring correction or adjustment.

Trial Balance

A ledger summary sheet where the sums of all accounts are organized into equal columns for both debits and credits.