A Two-Sample Z-Test for Two Population Proportions Is to Be

question 5

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is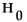
:
=
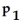
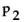
and the alternative is
:
≠
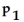
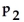
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-n₁ = 50 n₂ = 75
X₁ = 20 x₂ = 15

• A)P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal.
• B)P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation.
• C)P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation.
• D)P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation.
• E)P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.

---

Definitions:

Currency Exchange Rates

The exchange rate that determines how much of one currency is equivalent to another.

Functional Currency

The currency of the primary economic environment in which an entity operates, usually determining the currency of record for financial reporting.

Account Balances

The total amounts in financial accounts, reflecting the sum of all transactions like deposits and withdrawals, at any given time.

Exchange Rates

The valuation of one currency in terms of its equivalent in another currency.