A Two-Sample Z-Test for Two Population Proportions Is to Be

question 42

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is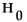
:
=
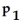
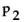
and the alternative is
:
≠
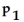
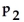
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-A poll reported that 30% of 60 Canadians between the ages of 25 and 29 had started saving money for retirement.Of the 40 Canadians surveyed between the ages of 21 and 24,25% had started saving for retirement.

• A)P-value = 0.5824;There is about a 58.24% chance that the two proportions are equal.
• B)P-value = 0.1812;If there is no difference in the proportions,there is about a 18.12% chance of seeing the observed difference or larger by natural sampling variation.
• C)P-value = 0.2912;There is about a 24.96% chance that the two proportions are equal.
• D)P-value = 0.2912;If there is no difference in the proportions,there is about a 24.96% chance of seeing the exact observed difference by natural sampling variation.
• E)P-value = 0.5824;If there is no difference in the proportions,there is about a 58.24% chance of seeing the observed difference or larger by natural sampling variation.

---

Definitions:

Blood

A vital fluid in humans and other animals that delivers necessary substances such as nutrients and oxygen to the cells and transport metabolic waste products away.

Accelerated Breathing Rates

An increase in the pace at which an individual breathes, often a response to exercise or stress.

Lactic Acid

A substance produced in the muscles during intense exercise, often associated with muscle fatigue and soreness.

Carbon Dioxide

A colorless, odorless gas produced by burning carbon and organic compounds and by respiration. It is naturally present in air and is absorbed by plants in photosynthesis.