A Two-Sample Z-Test for Two Population Proportions Is to Be

question 20

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is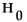
:
=
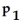
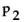
and the alternative is
:
≠
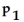
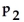
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-A university found it retained 25 students out of 352 in 2009 and 36 students out of 334 in 2010.

• A)P-value = 0.0455;If there is no difference in the proportions,there is about a 4.55% chance of seeing the observed difference or larger by natural sampling variation.
• B)P-value = 0.9545;If there is no difference in the proportions,there is about a 95.45% chance of seeing the observed difference or larger by natural sampling variation.
• C)P-value = 0.0455;There is about a 4.55% chance that the two proportions are equal.
• D)P-value = 0.091;There is about a 9.1% chance that the two proportions are equal.
• E)P-value = 0.091;If there is no difference in the proportions,there is about a 9.1% chance of seeing the observed difference or larger by natural sampling variation.

---

Definitions:

Iodide

A negative ion of iodine, often used in nutrition and medicine.

Thyroxine-binding Globulin

A plasma protein that transports thyroxine (T4) and triiodothyronine (T3) thyroid hormones in the bloodstream.

Thyroid Hormones

Hormones produced by the thyroid gland, crucial for regulating metabolism, energy generation, and growth.

Metabolized

The process of breaking down substances within the body to produce energy, or the conversion of substances into other forms within the body.