A Two-Sample Z-Test for Two Population Proportions Is to Be

question 18

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is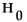
:
=
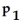
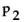
and the alternative is
:
≠
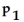
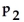
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-n₁ = 200 n₂ = 100
X₁ = 11 x₂ = 8

• A)P-value = 0.2005;There is about a 20.05% chance that the two proportions are equal
• B)P-value = 0.401;There is about a 40.1% chance that the two proportions are equal.
• C)P-value = 0.401;If there is no difference in the proportions,there is about a 40.1% chance of seeing the observed difference or larger by natural sampling variation.
• D)P-value = 0.2005;If there is no difference in the proportions,there is about a 20.05% chance of seeing the observed difference or larger by natural sampling variation.
• E)P-value = 0.401;If there is a difference in the proportions,there is a 40.1% chance of seeing the observed difference by natural sampling variation.

---

Definitions:

Homeless

The condition of lacking stable, safe, and adequate housing.

Schizophrenia

A long-term mental disorder characterized by disruptions in thought processes, perceptions, emotional responsiveness, and social interactions.

Percentage

A mathematical concept that represents a fraction of 100 as a figure of merit or loss in comparison.

Psychotherapy

A form of treatment involving psychological techniques, designed to improve mental health and resolve or mitigate troublesome behaviors, beliefs, feelings, and somatic responses.