A Two-Sample Z-Test for Two Population Proportions Is to Be

question 5

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is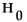
:
=
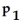
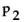
and the alternative is
:
≠
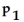
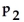
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-n₁ = 50 n₂ = 75
X₁ = 20 x₂ = 15

• A)P-value = 0.0073;There is about a 0.73% chance that the two proportions are equal.
• B)P-value = 0.0073;If there is no difference in the proportions,there is about a 0.73% chance of seeing the observed difference or larger by natural sampling variation.
• C)P-value = 0.0037;If there is no difference in the proportions,there is a 0.37% chance of seeing the exact observed difference by natural sampling variation.
• D)P-value = 0.0146;If there is no difference in the proportions,there is about a 1.46% chance of seeing the observed difference or larger by natural sampling variation.
• E)P-value = 0.0146;There is about a 1.46% chance that the two proportions are equal.

---

Definitions:

Budgeted Materials Cost

The projected cost of materials outlined in a budget, which is estimated before the actual purchase or use in production.

Finished Unit

A finished unit refers to a product that has completed the manufacturing process and is ready for sale or distribution to customers.

Ending Inventory

The total value of goods available for sale at the end of an accounting period, after factoring in purchases and costs.

Biodegradable Cleaning Product

A cleaning agent that can be decomposed by bacteria or other living organisms, reducing its impact on the environment.