A Two-Sample Z-Test for Two Population Proportions Is to Be

question 20

Multiple Choice

A two-sample z-test for two population proportions is to be performed using the P-value approach.The null hypothesis is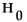
:
=
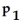
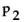
and the alternative is
:
≠
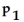
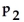
.Use the given sample data to find the P-value for the hypothesis test.Give an interpretation of the p-value.
-A university found it retained 25 students out of 352 in 2009 and 36 students out of 334 in 2010.

• A)P-value = 0.0455;If there is no difference in the proportions,there is about a 4.55% chance of seeing the observed difference or larger by natural sampling variation.
• B)P-value = 0.9545;If there is no difference in the proportions,there is about a 95.45% chance of seeing the observed difference or larger by natural sampling variation.
• C)P-value = 0.0455;There is about a 4.55% chance that the two proportions are equal.
• D)P-value = 0.091;There is about a 9.1% chance that the two proportions are equal.
• E)P-value = 0.091;If there is no difference in the proportions,there is about a 9.1% chance of seeing the observed difference or larger by natural sampling variation.

---

Definitions:

Product Knowledge

Detailed information about the features, benefits, and use of specific products which enables sales professionals to sell more effectively.

Leadership Styles

Describes the various approaches and methods leaders use to motivate, guide, and manage teams or organizations.

Classic Styles

Traditional or longstanding approaches or designs that have withstood the test of time in various fields such as fashion, architecture, or literature.

Fiedler's Contingency Theory

A leadership model proposing that effective leadership depends on the match between a leader's style of interacting with subordinates and the degree to which the situation gives control and influence to the leader.