Two Vectors 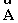and , Are Added Together to Form

question 65

Multiple Choice

Two vectors and , are added together to form the vector 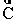= + 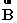. The relationship between the magnitudes of these vectors is given by: C_x = A cos 30° + B and C_y = -A sin 30°. Which statement best describes the orientation of these vectors?

• A) points in the negative x direction while points in the positive y direction.
• B) points in the negative y direction while points in the positive x direction.
• C) points 30° below the positive x axis while points in the positive x direction.
• D) points 30° above the positive x axis while points in the positive x direction.
• E) points 30° above the negative x axis while points in the positive x direction.

---

Definitions:

Entertainment Industry

A sector of the economy focused on the production and distribution of films, television shows, music, video games, and other forms of entertainment.

Social Commerce

The convergence of e-commerce with social media, enabling shopping through social media platforms.

Social Community

An online platform or group where individuals with common interests or goals interact, share ideas, and build relationships.