For H(x) = 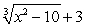, Find Two Functions P and Q

question 178

Multiple Choice

For H(x) = , find two functions p and q such that (p ◦ q) (x) = H(x) . (Answers my vary.)

• A) p(x) = x - 10 and q(x) =
• B) p(x) = x² - 10 and q(x) =
• C) p(x) = and q(x) = x² - 10
• D) p(x) = and q(x) = x - 10

---

Definitions:

Dissolved

The process of legally terminating the existence of an entity, such as a corporation or partnership, according to the laws of the jurisdiction in which it is registered.

Capital Contribution

Money, assets, or other resources a partner or shareholder provides to a company or partnership to increase its capital.

LLC Statutes

Laws and regulations that govern the formation, operation, and dissolution of Limited Liability Companies within a jurisdiction.

Articles of Organization

The document filed with a state governmental body to legally form a limited liability company (LLC).