You have learned that earnings functions are one of the most investigated relationships in economics. These typically relate the logarithm of earnings to a series of explanatory variables such as education, work experience, gender, race, etc.
(a)Why do you think that researchers have preferred a log-linear specification over a linear specification? In addition to the interpretation of the slope coefficients, also think about the distribution of the error term.
(b)To establish age-earnings profiles, you regress ln(Earn)on Age, where Earn is weekly earnings in dollars, and Age is in years. Plotting the residuals of the regression against age for 1,744 individuals looks as shown in the figure: 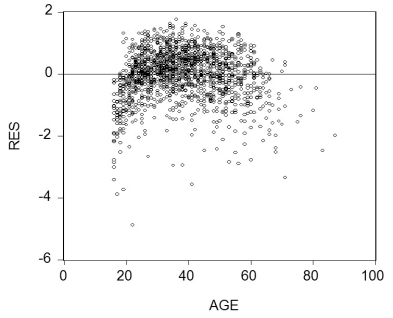 Do you sense a problem?
Do you sense a problem?
(c)You decide, given your knowledge of age-earning profiles, to allow the regression line to differ for the below and above 40 years age category. Accordingly you create a binary variable, Dage, that takes the value one for age 39 and below, and is zero otherwise. Estimating the earnings equation results in the following output (using heteroskedasticity-robust standard errors):
Sketch both regression lines: one for the age category 39 years and under, and one for 40 and above. Does it make sense to have a negative sign on the Age coefficient? Predict the ln(earnings)for a 30 year old and a 50 year old. What is the percentage difference between these two?
(d)The F-statistic for the hypothesis that both slopes and intercepts are the same is 124.43. Can you reject the null hypothesis?
(e)What other functional forms should you consider?
Definitions:
Own Analysis
Own analysis refers to the practice of self-examination or self-reflection to gain insights into one's thoughts, emotions, and behaviors.
Divine Intervention
Divine Intervention refers to the belief in spiritual forces or a deity intervening in human affairs, which can be a source of strength and comfort for some individuals.
Individuation
The process of becoming aware of oneself as an individual distinct from others and the general social environment.
Collaborative Educator Relationship
A partnership model between educators and others (students, parents, community members) emphasizing shared goals and mutual respect.
Q6: (Requires Calculus)For the simple linear regression
Q16: var(aX + bY)=<br>A) <span class="ql-formula"
Q30: The IV estimator can be used to
Q30: One of the major lessons learned in
Q30: In the regression model Y<sub>i</sub> = β<sub>0</sub>
Q33: You have estimated the relationship between
Q36: (Requires Advanced material)Maximum likelihood estimation yields the
Q37: The formulae for the AIC and the
Q52: The OLS formula for the slope
Q60: The following are all least squares assumptions