Sports Economics Typically Looks at Winning Percentages of Sports Teams

question 5

Essay

Sports economics typically looks at winning percentages of sports teams as one of various outputs, and estimates production functions by analyzing the relationship between the winning percentage and inputs. In Major League Baseball (MLB), the determinants of winning are quality pitching and batting. All 30 MLB teams for the 1999 season. Pitching quality is approximated by "Team Earned Run Average" (ERA), and hitting quality by "On Base Plus Slugging Percentage" (OPS).
Summary of the Distribution of Winning Percentage, On Base Plus Slugging Percentage,
and Team Earned Run Average for MLB in 1999 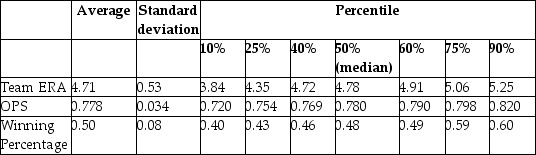Your regression output is:
$$\begin{array} { l } \widehat { \text { Winpct } } = - 0.19 - 0.099 \times \text { teamera } + 1.490 \times \text { ops, } R 2 = 0.92 , \text { SER } = 0.02 \text {. } \\\quad\quad\quad\quad\quad\text { (0.08) (0.008) }\quad\quad\quad\quad\quad\quad(0.126) \\\end{array}$$
(a)Interpret the regression. Are the results statistically significant and important?
(b)There are two leagues in MLB, the American League (AL)and the National League (NL). One major difference is that the pitcher in the AL does not have to bat. Instead there is a "designated hitter" in the hitting line-up. You are concerned that, as a result, there is a different effect of pitching and hitting in the AL from the NL. To test this hypothesis, you allow the AL regression to have a different intercept and different slopes from the NL regression. You therefore create a binary variable for the American League (DAL)and estimate the following specification: $\begin{aligned}\widehat { \text { Winpct } = - } & 0.29 + 0.10 \times D A L - 0.100 \times \text { teamera } + 0.008 \times ( \text { DAL } \times \text { teamera } ) \\& ( 0.12 ) ( 0.24 ) \quad\quad\quad\quad ( 0.008 )\quad\quad\quad\quad(0.018) \\\\& + 1.622 ^ { * } \text { ops } - 0.187 ^ { * } ( D A L \times \text { ops } ) , R 2 = 0.92 , S E R = 0.02 . \\& ( 0.163 ) \quad\quad\quad\quad ( 0.160 )\end{aligned}$
What is the regression for winning percentage in the AL and NL? Next, calculate the t-statistics and say something about the statistical significance of the AL variables. Since you have allowed all slopes and the intercept to vary between the two leagues, what would the results imply if all coefficients involving DAL were statistically significant?
(c)You remember that sequentially testing the significance of slope coefficients is not the same as testing for their significance simultaneously. Hence you ask your regression package to calculate the F-statistic that all three coefficients involving the binary variable for the AL are zero. Your regression package gives a value of 0.35. Looking at the critical value from you F-table, can you reject the null hypothesis at the 1% level? Should you worry about the small sample size?

---

Definitions:

Hypotonic Environment

An environment in which the concentration of solutes is lower outside the cell than inside, leading to water influx into the cell.

Rigid Cell Wall

A structural component found in plants, fungi, and certain bacteria, providing support and protection, often composed of cellulose in plants.

Efficient Water Pump

A device or system that minimizes energy consumption while maximizing the volume of water moved or lifted.

Basal Body

A structure derived from a centriole that forms the basis of a ciliary or flagellar structure in eukaryotic cells.