The Following Data Show the Demand for an Airline Ticket

question 26

Multiple Choice

The following data show the demand for an airline ticket dependent on the price of this ticket. For the assumed cubic and log-log regression models, Demand = β₀ + β₁Price + β₂Price² + β₃Price³ + ε and ln(Demand) = β₀ + β₁ln(Price) + ε, the following regression results are available. 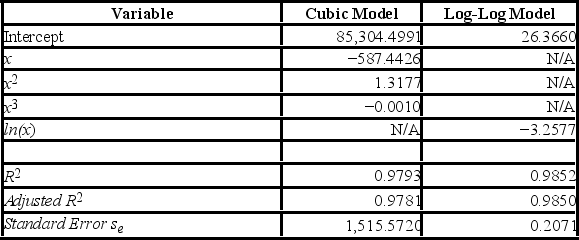Which of the following does the slope of the obtained log-log regression equation ln ( ) = 26.3660 - 3.2577 ln(Price) signify?

• A) For every 1% increase in the price, the predicted demand declines by approximately 3.2577%.
• B) For every 1% increase in the demand, the expected price increases by approximately 3.2577%.
• C) For every 1% increase in the demand, the expected price decreases by approximately 3.2577%.
• D) For every 1% increase in the price, the predicted demand increases by approximately 3.2577%.

Recognize the importance of family influence on educational aspirations compared to peer groups.

Know the concept of self-socialization and its impact on selecting socialization influences.

Analyze the rejection of the hidden curriculum by students from poor and racial minority families.

Understand that conflict between adolescents and parents is often temporary and influenced by external perceptions.

---

Definitions:

Minority Groups

Demographic groups that are smaller in numbers within a larger population and may face disparities in economic, political, or social opportunities.

Chronic Illness

a long-lasting health condition that may not have a cure, impacting the individual's lifestyle and possibly requiring ongoing treatment.

U.S. Population

The total number of people living in the United States, including all ethnicities and demographic segments.

Older Than 65

The demographic group classified as senior citizens, typically associated with the age at which one is considered eligible for government-assisted retirement benefits.