Examlex

Solved

Quarterly Sales of a Department Store for the Last Seven

question 40

Essay

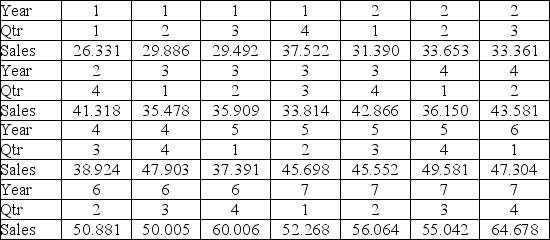
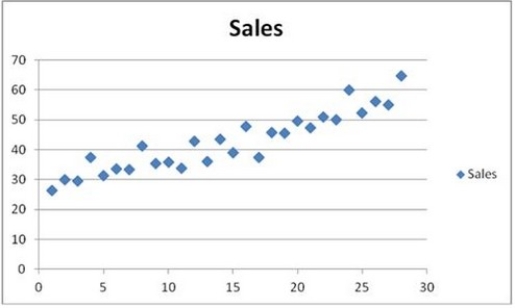Quarterly sales of a department store for the last seven years are given in the following table. Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β0 + β1Qtr1 + β2Qtr2 + β3Qtr3 + β4t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. 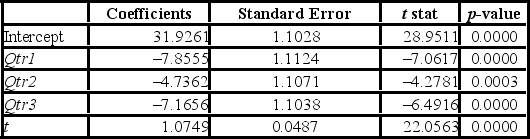Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? t = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? t = Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? t × Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? t with Quarterly sales of a department store for the last seven years are given in the following table. The scatterplot shows that the quarterly sales have an increasing trend and seasonality. A linear regression model given by Sales = β<sub>0</sub> + β<sub>1</sub>Qtr1 + β<sub>2</sub>Qtr2 + β<sub>3</sub>Qtr3 + β<sub>4</sub>t + ε, where t is the time period (t = 1, ..., 28) and Qtr1, Qtr2, and Qtr3 are quarter dummies, is estimated and then used to make forecasts. For the regression model, the following partial output is available. Using MSE and MAD, compare the linear trend equation with seasonal dummy variables, <sub>t</sub> = 31,9261 - 7.855Qtr1 - 4.7362Qtr2 - 7.1656Qtr3 + 1.0749t, and the decomposition method equation <sub>t</sub><sub> </sub>= <sub>t </sub>× <sub>t</sub><sub> </sub>with t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended? t = 26.8819 + 1.0780t and the quarterly seasonal indices: 0.9322, 1.0066, 0.9441, and 1.1171. Which of the two corresponding forecasting models is recommended?

Definitions:

Related Questions

Q28: A realtor wants to predict and compare

Q31: Which of the following equations is a

Q52: Typically, the sales volume declines with an

Q75: The only possible income from an investment

Q78: For the Kruskal-Wallis test with n<sub>i</sub> ≥

Q82: For the Spearman rank correlation test we

Q89: The seller of a put option:<br>A)has the

Q93: Refer to below regression results. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6618/.jpg"

Q99: A long straddle is a strategy that

Q109: Investment institutions usually have funds with different