Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 52

True/False

Instruction 12.35
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$



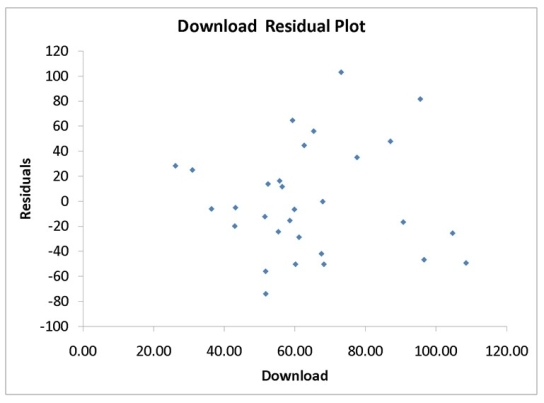
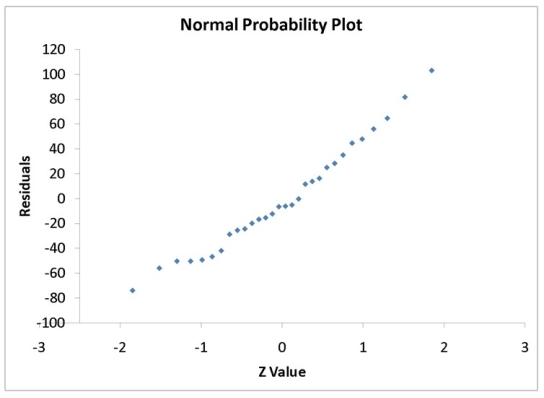
-Referring to Instruction 12.35,the null hypothesis that there is no linear relationship between revenue and number of downloads should be rejected at a 5% level of significance.

---

Definitions:

Algorithm

A process or set of rules to be followed in calculations or other problem-solving operations, especially by a computer.

Mental Image

A representation of a sensory experience in the mind, which can be visual, auditory, or related to other senses, even in the absence of external stimuli.

Dialectical Reasoning

A method of argument for resolving disagreement that involves the exchange of arguments and counter-arguments, aiming to find the truth through reasoned dialogue.

Contextual Intelligence

The aptitude to understand and apply knowledge effectively across varied situations by keenly evaluating the contextual factors.