Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 163

True/False

Instruction 12.26
The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application. Data are collected from a sample of 30 days, and the number of applications recorded and completion time in hours is recorded. Below is the regression output:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline\text { MultipleR } & 0.9447 \\\hline \text { R Square } & 0.8924 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.8886 \\\hline \text { Standard Error } & 0.3342 \\\hline \text { Observations } & 30 \\\hline\end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S 5 & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm{E}-15 \\\hline \text { Residual } & 28 & 3.1282 & 0.1117 & & \\\hline \text { Total } & 29 & 29.072 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { tStat } & \text { p-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\hline \begin{array}{l}\text { Applications } \\\text { Recorded }\end{array} & 0.0126 & 0.0008 & 15.2388 & \begin{array}{l}4.3946 \mathrm{E}- \\15\end{array} & 0.0109 & 0.0143 \\\hline\end{array}$



Note: 4.3946E-15 is 4.3946 × 10^-15.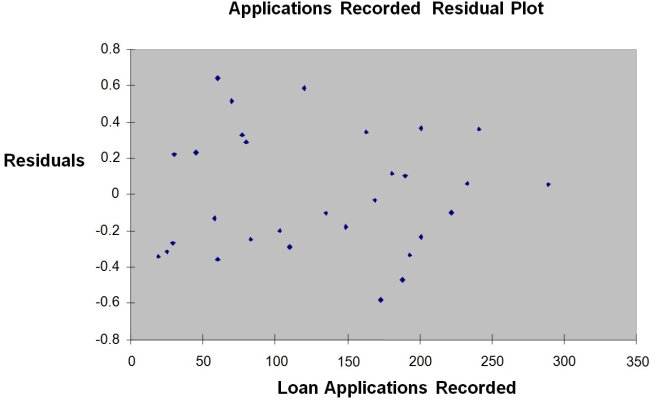
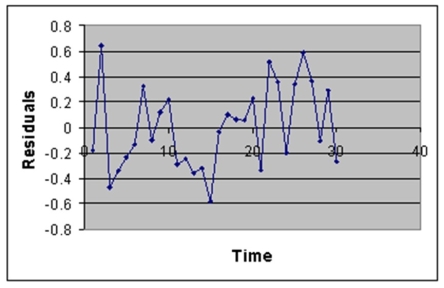
-Referring to Instruction 12.26,there is no evidence of positive autocorrelation if the Durbin-Watson test statistic is found to be 1.78.

---

Definitions:

Utility Maximizing

The process or behavior of consumers attempting to get the greatest amount of satisfaction from their consumption choices, subject to their income and the prices of goods and services.

Consumption Map

A graphical representation showing different combinations of goods or services that provide equal satisfaction or utility to a consumer.

Budget Line

The budget line represents the combinations of two goods that a consumer can purchase with a given budget, taking into account the prices of the goods.

Consumer Preference

Individuals' or groups' choices and priorities regarding products, services, or other consumption activities.