Instruction 12 $\text { Regression statistics }$ $\text { ANOVA }$

question 141

True/False

Instruction 12.35
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\text { Regression statistics }$
$\begin{array}{|l|l|}\hline \text { MultipleR } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \begin{array}{l}\text { Adjusted R } \\\text { Square }\end{array} & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000\\\hline \end{array}$

$\text { ANOVA }$
$\begin{array}{|l|l|l|l|l|l|}\hline & d f & S S & M S & F & \begin{array}{l}\text { Significance } \\F\end{array} \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{|l|l|l|l|l|l|l|}\hline & \text { Coefficients } & \begin{array}{l}\text { Standard } \\\text { Error }\end{array} & \text { t Stat } & p \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$



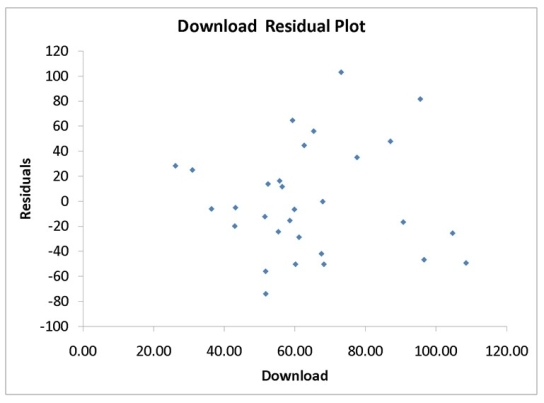
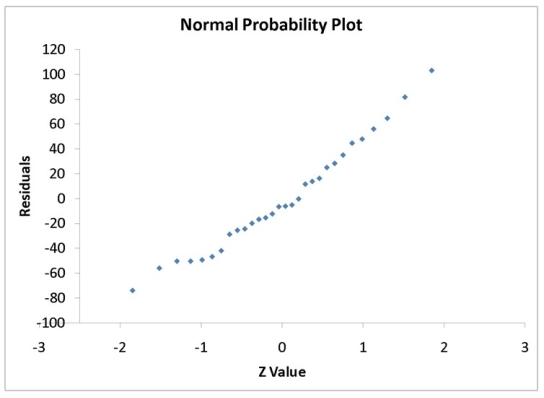
-Referring to Instruction 12.35,there is sufficient evidence that revenue and number of downloads are linearly related at a 5% level of significance.

---

Definitions:

Federal Income Taxes

Taxes levied by the federal government on the annual earnings of individuals, corporations, trusts, and other legal entities.

Credit Sales

Transactions where goods or services are provided to a customer with the agreement that payment will be made at a later date.

Uncollectible

Refers to accounts receivable that are considered to be uncollectable and are thus written off as a bad debt expense.

Cash Receipts

The collection of money (currency, checks, wire transfers) by a business from its customers or other parties.