Instruction 13 $Y =$ Weight-Loss (In Kilograms) $X _ { 1 } =$

question 45

Multiple Choice

Instruction 13.38
A weight-loss clinic wants to use regression analysis to build a model for weight-loss of a client (measured in kilograms) . Two variables thought to effect weight-loss are client's length of time on the weight loss program and time of session. These variables are described below:
$Y =$ Weight-loss (in kilograms)
$X _ { 1 } =$ Length of time in weight-loss program (in months)
$x _ { 2 } = 1$ if morning session, 0 if not
$x _ { 3 } = 1$ if afternoon session, 0 if not (Base level = evening session)
Data for 12 clients on a weight-loss program at the clinic were collected and used to fit the interaction model:
$$Y = \beta 0 + \beta _ { 1 } X _ { 1 } + \beta _ { 2 } X _ { 2 } + \beta _ { 3 } X _ { 3 } + \beta _ { 4 } X _ { 1 } X _ { 2 } + \beta _ { 5 } X _ { 1 } X _ { 3 } + \varepsilon$$
Partial output from Microsoft Excel follows:

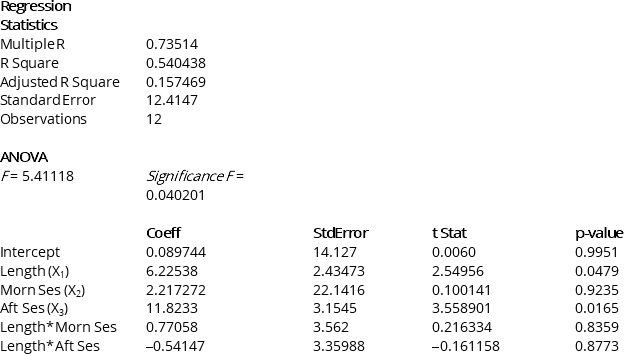
-Referring to Instruction 13.38,what null hypothesis would you test to determine whether the slope of the linear relationship between weight-loss (Y) and time in the program (X₁) varies according to time of session?

• A) H₀: \(\beta\)₂ = \(\beta\)₃ = 0
• B) H₀: \(\beta\)₄ = \(\beta\)₅ = 0
• C) H₀: \(\beta\)₁ = \(\beta\)₂ = \(\beta\)₃ = \(\beta\)₄ = \(\beta\)₅ = 0
• D) H₀: \(\beta\)₂ = \(\beta\)₃ = \(\beta\)₄ = \(\beta\)₅ = 0

---

Definitions:

Marginal Products

The additional output that results from using one more unit of a production input, keeping all other inputs constant.

Total Product

Total Product refers to the overall quantity of output that a firm produces, usually with respect to a given quantity of inputs over a specific period of time.

Marginal Products

The additional output produced as a result of utilizing one more unit of a particular input.

Marginal Product

It is the increase in output that results from a one-unit increase in the input, keeping all other inputs constant.