The Cube of Insulating Material Shown in the Figure Has

question 981

Short Answer

The cube of insulating material shown in the figure has one corner at the origin.Each side of the cube has length 0.080 m so the top face of the cube is parallel to the xz-plane and is at y = 0.080 m.It is observed that there is an electric field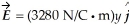
that is in the +y direction and whose magnitude depends only on y.Use Gauss's law to calculate the net charge enclosed by the cube.
(ε₀ = 8.85 × 10^-12 C²/N • m²)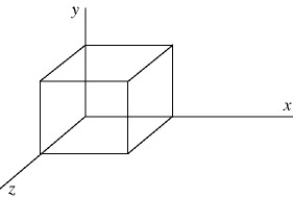

---

Definitions:

Binomial Distribution

A probability distribution that summarizes the likelihood that a value will take one of two independent states under a given number of trials.

Sampling Distribution

Sampling Distribution is the probability distribution of a given statistic based on a random sample, used to make inferences about a population.

Sample Proportion

The ratio of members in a sample exhibiting a certain trait to the total number of members in the sample.

Central Limit Theorem

A principle stating that the distribution of sample means approaches a normal distribution as the sample size becomes larger, regardless of the population's distribution.