Examlex

Solved

The Random Variable X Has the Cumulative Distribution Function F(x)whose

question 3

Essay

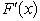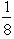The random variable X has the cumulative distribution function F(x)whose value or derivative The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. 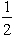is shown below for various values of x.F(0)= 0, The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. 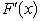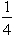= The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. 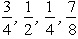,for 0 < x < 2,P(X = 2)= The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. 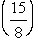,so F(2)= The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. , The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. = The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. .Also calculate the sample average and compare it with the true mean The random variable X has the cumulative distribution function F(x)whose value or derivative is shown below for various values of x.F(0)= 0, = ,for 0 < x < 2,P(X = 2)= ,so F(2)= , = ,for 2 < x < 3,F(3)= 1.Generate four random observations from this probability distribution by using the following uniform random numbers: .Also calculate the sample average and compare it with the true mean for this probability distribution. for this probability distribution.

Definitions:

Multiple Linear Regression

An analytical approach in statistics that uses a linear equation to define how a dependent variable is related to two or more independent variables based on observed data.

Alternative Hypothesis

A statement that contradicts the null hypothesis and is tested to determine if there is evidence to support it.

Mean Difference

Mean difference, also known as the average difference, refers to the arithmetic mean of differences between paired observations in two sample sets.

Same Individuals

Referring to using the same group of subjects or samples in different conditions or periods of a study or experiment.

Related Questions

Q2: According to the absorption approach,an increase in

Q12: An "automatic" adjustment mechanism would require a

Q13: Under an adjustable-pegged system,market exchange rates are

Q39: Concerning international debt,_ refers to a negotiated

Q44: By the early 1970s,gold had been phased

Q49: The foreign-trade multiplier equals the sum of

Q56: Who makes up the project development team

Q71: Which type of relationship cardinality requires the

Q82: The U.S.dollar,Japanese yen,British pound,and Mexican peso are

Q84: Which consideration is not of concern in