Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Homoscedasticity of Error Assumption Appears to the Number

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Homoscedasticity of Error Assumption Appears to the Number

Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Homoscedasticity of Error Assumption Appears to the Number

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Homoscedasticity of Error Assumption Appears to the Number

Solved

Instruction 12-11
a Computer Software Developer Would Like to Use

question 72

True/False

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\text { Standard Error } & 44.4765 \\\text { Observations } & 30.0000\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r|}\hline&df&SS&MS&F&\text {significance F}\\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & &\\\hline\end{array}$
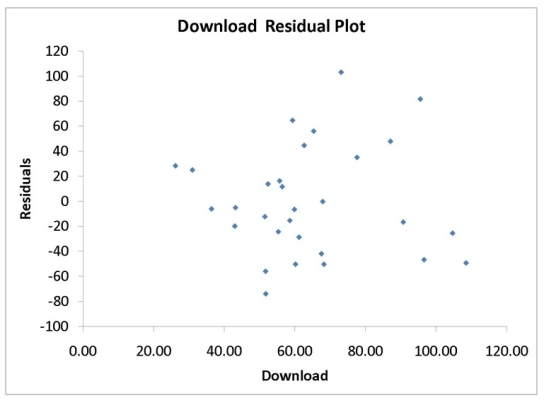
$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} \hline&df&SS&MS&F&\text {significance F}\\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & &\\\hline \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the homoscedasticity of error assumption appears to have been violated.$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} \hline&df&SS&MS&F&\text {significance F}\\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & &\\\hline \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the homoscedasticity of error assumption appears to have been violated.$
-Referring to Instruction 12-11,the homoscedasticity of error assumption appears to have been violated.

Definitions:

Movement Inhibition

The suppression or delay of an action or movement, which can be a voluntary decision or a result of neurological mechanisms.

Putamen

A round structure located at the base of the forebrain and part of the basal ganglia, involved in motor control and learning.

Globus Pallidus

A subcortical structure located in the brain, involved in the regulation of voluntary movement by influencing the thalamus.

Nigrostriatal Dopamine System

A pathway in the brain involved in the control of movement; degeneration of this system is associated with Parkinson's disease.