Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis for Testing Whether There

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis for Testing Whether There

Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis for Testing Whether There

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis for Testing Whether There

Solved

Instruction 12-11
a Computer Software Developer Would Like to Use

question 171

True/False

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r|}& d f & \text { SS } & {M S} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\\hline \text { Total } & 29 & 226451.3503 & &\end{array}$

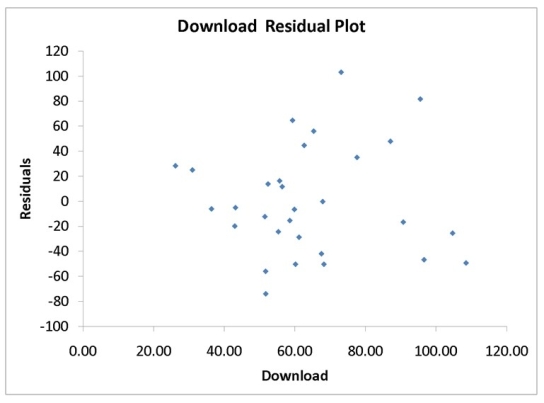
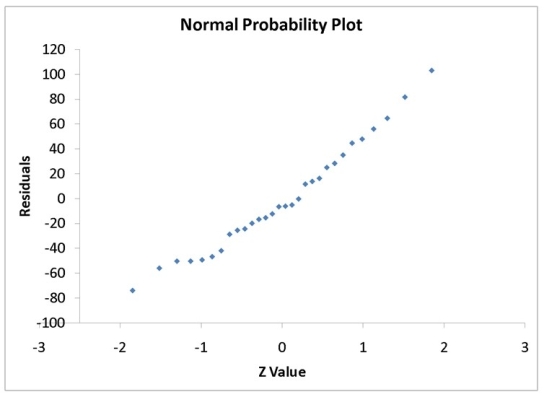
$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the null hypothesis for testing whether there is a linear relationship between revenue and number of dowloads is There is no linear relationship between revenue and number of downloads .$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the null hypothesis for testing whether there is a linear relationship between revenue and number of dowloads is There is no linear relationship between revenue and number of downloads .$
-Referring to Instruction 12-11,the null hypothesis for testing whether there is a linear relationship between revenue and number of dowloads is "There is no linear relationship between revenue and number of downloads".

Definitions:

Mid-Level

Pertains to a position, status, or area that is in between the highest and the lowest levels, often implying a moderate degree of complexity or authority.

Grand

Large, magnificent, or impressive in size, appearance, or style.

Parsimonious

Describing an explanation or theory that is simple and lacks unnecessary elements, often preferred for its efficiency and effectiveness in problem-solving.

Mini Theories

Specific, narrow theories that address particular aspects of behavior rather than broad, overarching models.