Instruction 12-11
a Computer Software Developer Would Like to Use

question 59

Multiple Choice

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r|}& d f & \text { SS } & {M S} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\\hline \text { Total } & 29 & 226451.3503 & &\end{array}$

$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$
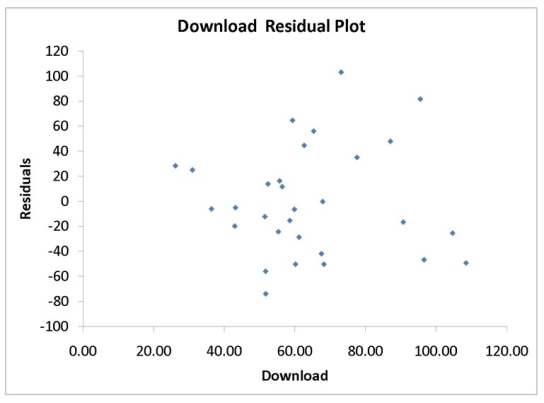
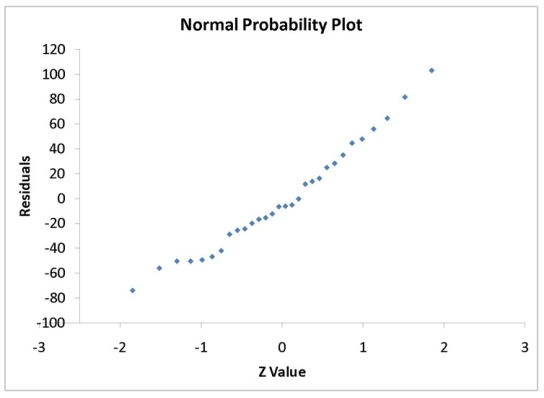
-Referring to Instruction 12-11,which of the following is the correct alternative hypothesis for testing whether there is a linear relationship between revenue and number of downloads?

• A)H₁: b₁ = 0
• B)H₁: ?₁ ? 0
• C)H₁: b₁ ? 0
• D)H₁: ?₁ = 0

---

Definitions:

Fiscal Year

A one-year period that companies and governments use for financial reporting and budgeting, different from a calendar year.

Straight-Line Method

The straight-line method is an accounting technique used to allocate the cost of an asset evenly over its useful life for the purposes of depreciation.

Semiannual Interest

The interest on a financial obligation, such as a bond or loan, that is paid twice a year.

Fiscal Year

A one-year period companies use for accounting purposes and preparing financial statements, which may or may not align with the calendar year.