Solved

Instruction 12-12
the Manager of the Purchasing Department of a Large

question 78

Multiple Choice

Instruction 12-12
The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output:
$\begin{array}{l}\begin{array} { l r } \hline { \text { Regression Statistics } } \\\hline \text { Multiple R } & 0.9447 \\\text { R Square } & 0.8924 \\\text { Adjusted R } & 0.8886 \\\text { Square } & \\\text { Standard } & 0.3342 \\\text { Error } & 30 \\\text { Observations } & \\\hline\end{array}\\\text { ANOVA }\\\begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\F\end{array} } \\\hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\\text { Residual } & 28 & 3.1282 & 0.1117 & & \\\text { Total } & 29 & 29.072 & & & \\\hline\end{array}\\\begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\\text { Error }\end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\\text { Applications RECORD } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143\\\hline\end{array}\end{array}$ Note: 4.3946E-15 is 4.3946 x 10^-15.
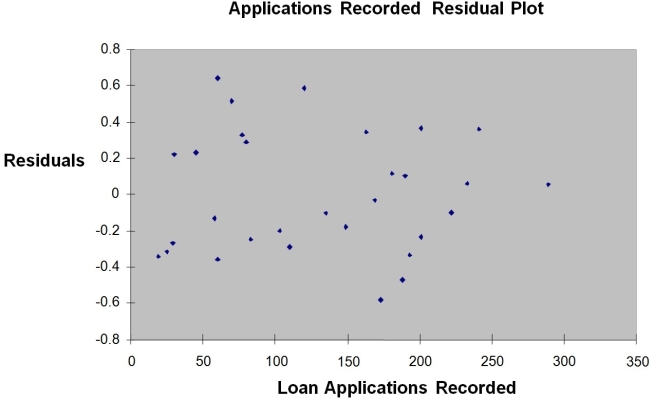
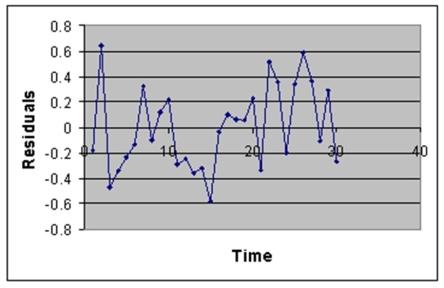
$Instruction 12-12 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output: \begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.9447 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R } & 0.8886 \\ \text { Square } & \\ \text { Standard } & 0.3342 \\ \text { Error } & 30 \\ \text { Observations } & \\ \hline \end{array}\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\ F \end{array} } \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & & \\ \hline \end{array}\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text { Applications RECORD } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143\\ \hline \end{array} \end{array} Note: 4.3946E-15 is 4.3946 x 10<sup>-15</sup>. -Referring to Instruction 12-12,the p-value of the measured t test statistic to test whether the number of loan applications recorded affects the amount of time is A) 4.3946E - 15. B) 0.0030. C) (0.0030) / 2. D) (4.3946E - 15) / 2.$ $Instruction 12-12 The manager of the purchasing department of a large savings and loan organization would like to develop a model to predict the amount of time (measured in hours) it takes to record a loan application.Data are collected from a sample of 30 days,and the number of applications recorded and completion time in hours is recorded.Below is the regression output: \begin{array}{l} \begin{array} { l r } \hline { \text { Regression Statistics } } \\ \hline \text { Multiple R } & 0.9447 \\ \text { R Square } & 0.8924 \\ \text { Adjusted R } & 0.8886 \\ \text { Square } & \\ \text { Standard } & 0.3342 \\ \text { Error } & 30 \\ \text { Observations } & \\ \hline \end{array}\\ \text { ANOVA }\\ \begin{array} { l r r r r r } \hline & d f & { \text { SS } } & { \text { MS } } & F & { \begin{array} { c } \text { Significance } \\ F \end{array} } \\ \hline \text { Regression } & 1 & 25.9438 & 25.9438 & 232.2200 & 4.3946 \mathrm { E } - 15 \\ \text { Residual } & 28 & 3.1282 & 0.1117 & & \\ \text { Total } & 29 & 29.072 & & & \\ \hline \end{array}\\ \begin{array} { l r r r r r r } \hline & \text { Coefficients } & \begin{array} { c } \text { Standard } \\ \text { Error } \end{array} & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \text { Intercept } & 0.4024 & 0.1236 & 3.2559 & 0.0030 & 0.1492 & 0.6555 \\ \text { Applications RECORD } & 0.0126 & 0.0008 & 15.2388 & 4.3946 \mathrm{E}-15 & 0.0109 & 0.0143\\ \hline \end{array} \end{array} Note: 4.3946E-15 is 4.3946 x 10<sup>-15</sup>. -Referring to Instruction 12-12,the p-value of the measured t test statistic to test whether the number of loan applications recorded affects the amount of time is A) 4.3946E - 15. B) 0.0030. C) (0.0030) / 2. D) (4.3946E - 15) / 2.$
-Referring to Instruction 12-12,the p-value of the measured t test statistic to test whether the number of loan applications recorded affects the amount of time is

Explain the implications of practice, fatigue, and other performance-related effects in repeated measures.

Understand the fundamental differences and applications between repeated measures and matched pairs designs.

Identify and explain key considerations in designing experiments involving repeated measures, such as the order of conditions, time intervals between treatments, and counterbalancing.

Understand the process and rationale behind using matched pairs design, including the importance of matching variables related to the dependent variable.

Definitions:

Equilibrium Price

The price at which the supply of an item equals the demand for it, resulting in no excess supply or demand.

Binding Price Ceiling

A maximum price set by the government below the equilibrium price, leading to shortages as the demand exceeds supply.

Quantity Demanded

The total amount of a good or service that consumers are willing and able to purchase at a given price level in a given time period.

Quantity Supplied

The total amount of a good or service that producers are willing and able to sell at a given price within a specified time period.

Instruction 12-12 the Manager of the Purchasing Department of a Large

Definitions:

Instruction 12-12
the Manager of the Purchasing Department of a Large