Instruction 12-11
a Computer Software Developer Would Like to Use

question 83

Multiple Choice

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\text { Standard Error } & 44.4765 \\\text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{lr|r|r|r|r}\hline & d f & {\text { SS }} &{\text { MS }} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Emor } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$
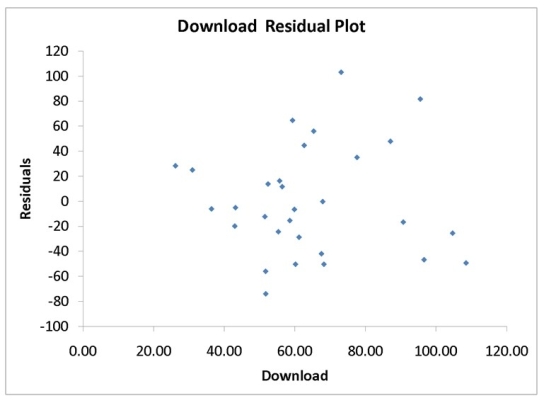
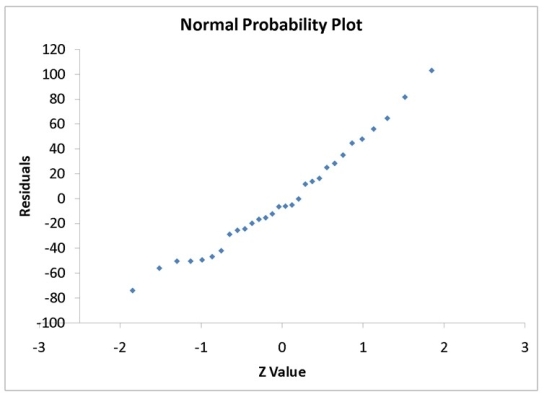
-Referring to Instruction 12-11,which of the following is the correct interpretation for the coefficient of determination?

• A)74.67% of the variation in revenue can be explained by the variation in the number of downloads.
• B)75.54% of the variation in revenue can be explained by the variation in the number of downloads.
• C)75.54% of the variation in the number of downloads can be explained by the variation in revenue.
• D)74.67% of the variation in the number of downloads can be explained by the variation in revenue.

---

Definitions:

Intonation

The variation of pitch in speech, which can convey different meanings, emotions, or nuances in verbal communication.

Intonation

The variation in pitch during speech, influencing the meaning and emotion of the spoken words.

Pitch

The perceived frequency of a sound, determining how high or low it sounds.

Volume

The level of sound intensity or loudness, often considered in communication to emphasize or convey emotion.