Instruction 12-11
a Computer Software Developer Would Like to Use

question 38

Short Answer

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\text { Standard Error } & 44.4765 \\\text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{lr|r|r|r|r}\hline & d f & {\text { SS }} &{\text { MS }} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & & \\\hline\end{array}$

$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Emor } & t \text { Stat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \\\hline\end{array}$
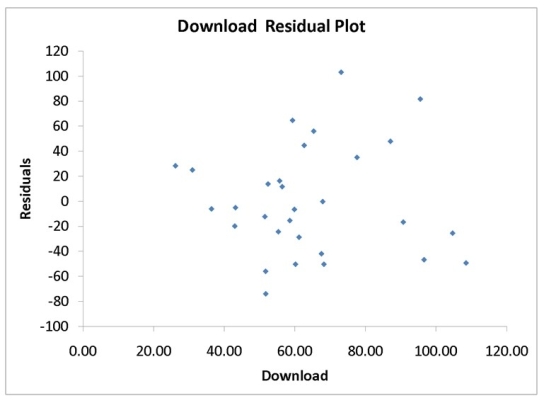
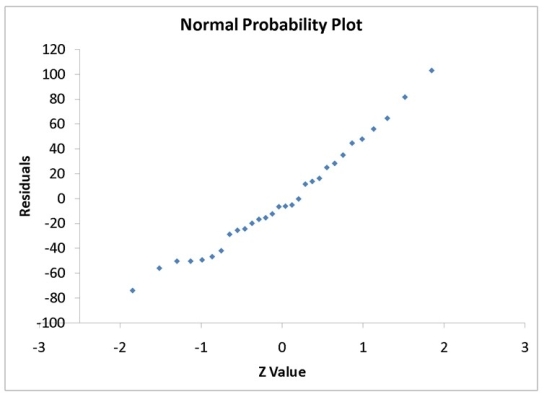
-Referring to Instruction 12-11,what is the standard deviation around the regression line?

---

Definitions:

Tracheids

Tracheids are elongated cells in the xylem of vascular plants, serving to transport water and minerals as well as providing structural support.

Carbohydrates

Organic compounds made up of carbon, hydrogen, and oxygen, serving as a major source of energy for living organisms, and found in foods as sugars, starches, and fiber.

Preprophase Band

In plant cells, a dense array of microtubules just inside of the plasma membrane that appears just prior to mitosis and determines the plane in which the cell will divide.

Mitosis

Mitosis is a cell division process that results in two genetically identical daughter cells from a single parent cell, crucial for growth and tissue repair.