Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Durbin-Watson Statistic Is Inappropriate for This

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Durbin-Watson Statistic Is Inappropriate for This

Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Durbin-Watson Statistic Is Inappropriate for This

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Durbin-Watson Statistic Is Inappropriate for This

Solved

Instruction 12-11
a Computer Software Developer Would Like to Use

question 167

True/False

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{|lr|}\hline{\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\text { Standard Error } & 44.4765 \\\text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r} & {\text { df }} & {\text { SS }} & {\text { MS }} & F & \text { Significance F } \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\\hline \text { Total } & 29 & 226451.3503 & & &\end{array}$

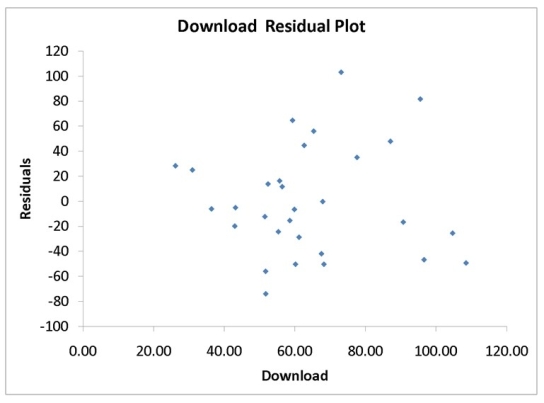
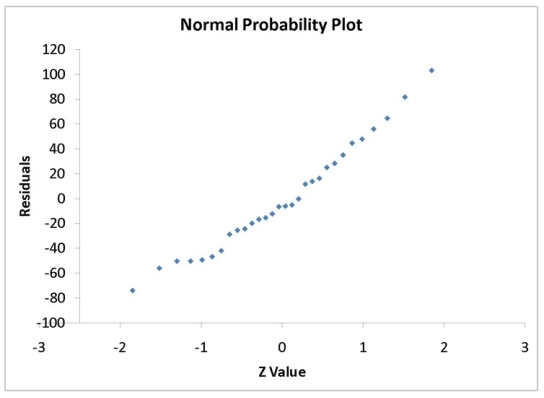
$\begin{array}{lrrrrrr}\hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & {\text { Lower 95\% }} & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{|lr|} \hline{\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r} & {\text { df }} & {\text { SS }} & {\text { MS }} & F & \text { Significance F } \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & {\text { Lower 95\% }} & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the Durbin-Watson statistic is inappropriate for this data set.$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{|lr|} \hline{\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \text { Standard Error } & 44.4765 \\ \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r} & {\text { df }} & {\text { SS }} & {\text { MS }} & F & \text { Significance F } \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \\ \hline \text { Total } & 29 & 226451.3503 & & & \end{array} \begin{array}{lrrrrrr} \hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & \text { P-value } & {\text { Lower 95\% }} & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the Durbin-Watson statistic is inappropriate for this data set.$
-Referring to Instruction 12-11,the Durbin-Watson statistic is inappropriate for this data set.

Definitions:

Collective Unconscious

A concept in psychoanalytic theory referring to a part of the unconscious mind that is shared among beings of the same species, containing ancestral memories.

Carl Jung

A Swiss psychiatrist and psychoanalyst who founded analytical psychology, known for his theories of the collective unconscious, archetypes, and psychological types.

Personality Functioning

Refers to the adaptive and maladaptive patterns of thinking, feeling, and behaving that characterize an individual.

Self-Disclosing

The act of revealing personal information about oneself to others.