Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis That There Is No

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis That There Is No

Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis That There Is No

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,the Null Hypothesis That There Is No

Solved

Instruction 12-11
a Computer Software Developer Would Like to Use

question 4

True/False

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r|}& d f & \text { SS } & {M S} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\\hline \text { Total } & 29 & 226451.3503 & &\end{array}$

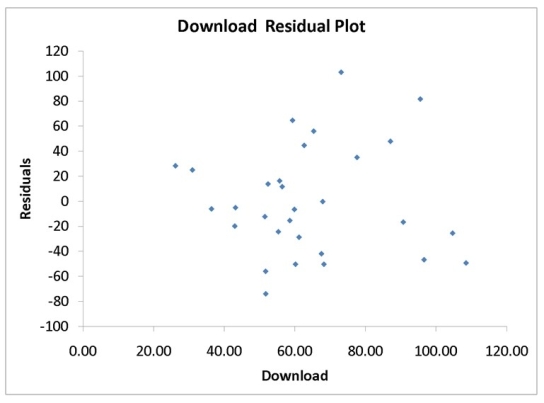
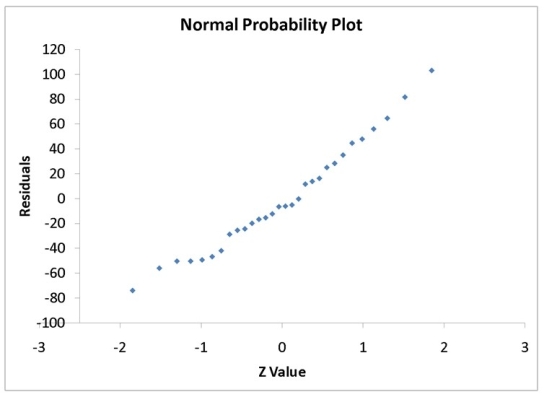
$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the null hypothesis that there is no linear relationship between revenue and number of downloads should be rejected at a 5% level of significance.$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,the null hypothesis that there is no linear relationship between revenue and number of downloads should be rejected at a 5% level of significance.$
-Referring to Instruction 12-11,the null hypothesis that there is no linear relationship between revenue and number of downloads should be rejected at a 5% level of significance.

Definitions:

Horizontal Axis

A line that runs left to right across the chart or graph, often used to represent the independent variable in a data set.

Indifference Curve

A graph representing different bundles of goods between which a consumer is indifferent, showing the trade-offs or substitutions a consumer is willing to make.

Midterm Grade

An academic performance indicator, usually given halfway through a course, reflecting a student's progress and achievements to that point.

Horizontal Axis

In a graph or chart, the x-axis, which typically represents the independent variable or the variable that is controlled or manipulated.