Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,what Is the P-Value for Testing Whether

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,what Is the P-Value for Testing Whether

Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,what Is the P-Value for Testing Whether

The Answer of Instruction 12-11 a Computer Software Developer Would Like to UseANOVA-Referring to Instruction 12-11,what Is the P-Value for Testing Whether

Solved

Instruction 12-11
a Computer Software Developer Would Like to Use

question 54

Short Answer

Instruction 12-11
A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
$\begin{array}{lr}\hline {\text { Regression Statistics }} \\\hline \text { Multiple R } & 0.8691 \\\hline \text { R Square } & 0.7554 \\\hline \text { Adjusted R Square } & 0.7467 \\\hline \text { Standard Error } & 44.4765 \\\hline \text { Observations } & 30.0000 \\\hline\end{array}$
ANOVA
$\begin{array}{|l|r|r|r|r|r|}& d f & \text { SS } & {M S} & F & \text { Significance } F \\\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\\hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\\hline \text { Total } & 29 & 226451.3503 & &\end{array}$

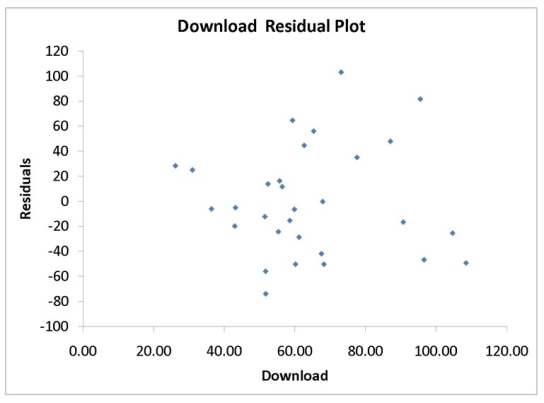
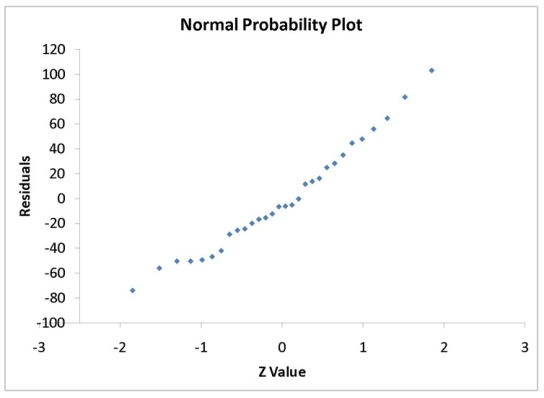
$\begin{array}{lrrrrrrr}\hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\\hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\\hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513\end{array}$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,what is the p-value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?$ $Instruction 12-11 A computer software developer would like to use the number of downloads (in thousands)for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars)he can make on the full version of the new shareware.Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: \begin{array}{lr} \hline {\text { Regression Statistics }} \\ \hline \text { Multiple R } & 0.8691 \\ \hline \text { R Square } & 0.7554 \\ \hline \text { Adjusted R Square } & 0.7467 \\ \hline \text { Standard Error } & 44.4765 \\ \hline \text { Observations } & 30.0000 \\ \hline \end{array} ANOVA \begin{array}{|l|r|r|r|r|r|} & d f & \text { SS } & {M S} & F & \text { Significance } F \\ \hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \\ \hline \text { Residuall } & 28 & 55388.4309 & 1978.1582 & \\ \hline \text { Total } & 29 & 226451.3503 & & \end{array} \begin{array}{lrrrrrrr} \hline & \text { Coefficients } & \text { Standard Eror } &{t \text { Stat }} & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \\ \hline \text { Intercept } & -95.0614 & 26.9183 & -3.5315 & 0.0015 & -150.2009 & -39.9218 \\ \hline \text { Download } & 3.7297 & 0.4011 & 9.2992 & 0.0000 & 2.9082 & 4.5513 \end{array} -Referring to Instruction 12-11,what is the p-value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?$
-Referring to Instruction 12-11,what is the p-value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?

Definitions:

Account

A registered user profile within a system or service that stores personal data, preferences, and is protected by credentials.

Folder Sharing

The process of granting other users access to view, modify, or collaborate on files contained within a specific folder on a computer or online platform.

Standard User Mode

A computer operating mode in which the user has permissions to perform ordinary tasks but lacks the ability to make changes that could affect the system's security or stability.

Picture Password

A security feature where users can unlock their device or account by performing specific gestures on a selected image.