Here Are Plots of Data for Studentized Residuals Against Length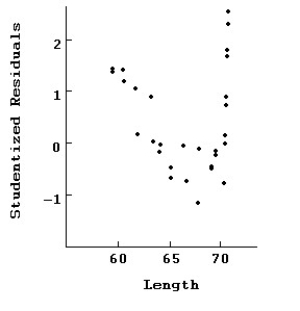

question 8

Essay

Here are plots of data for Studentized residuals against Length. Here is the same regression with all of the points at 70 removed.
Dependent variable is: Weight
30 total bears of which 10 are missing
R-squared = 97.8% R-squared (adjusted)= 97.3%
s = 2.96 with 20 - 4 = 16 degrees of freedom $$\begin{array} { l r r r r } & \text { Sum of } & & { \text { Mean } } \\\text { Source } & \text { Squares } & \text { DF } & \text { Square } & \text { F-ratio } \\\text { Regression } & 7455.0 & 3 & 2485 & 238.26 \\\text { Residual } & 166.89 & 16 & 10.43 &\end{array}$$ $$\begin{array} { l r c r r } \text { Variable } & \text { Coefficient } & \text { SE(Coeff) } & \text { t-ratio } & \text { P-value } \\\text { Intercept } & - 169.16 & 3.23 & - 52.37 & < 0.0001 \\\text { Chest } & 0.84 & 0.58 & 1.45 & 0.1590 \\\text { Length } & 5.59 & 2.14 & 2.61 & 0.0148 \\\text { Sex } & - 1.19 & 1.98 & - 0.60 & 0.5537\end{array}$$ Compare the regression with the previous one.In particular,which model is likely to make the best prediction of weight? Which seems to fit the data better?

---

Definitions:

Personal Liability

The legal responsibility of an individual to settle debts or obligations from their own assets, rather than those protected by a corporation or limited liability entity.

Business Debts

Obligations that a business incurs as a result of operating activities, including loans, accounts payable, and any other form of borrowed money.

No Personal Liability

A legal principle that protects individual actors within a corporation or legal entity from bearing personal financial responsibility for the entity's liabilities.

Agency Relationships

A legal arrangement where one party, the agent, acts on behalf of another party, the principal, in transactions with third parties.