Use the Figure to Approximate the Trigonometric Values to Within $\cos 3$

question 2

Multiple Choice

Use the figure to approximate the trigonometric values to within successive tenths. Then use a calculator to compute the values to the nearest hundredth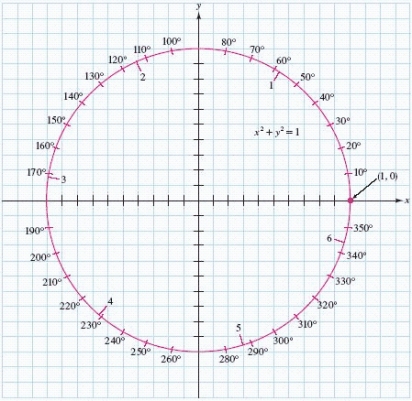. $\cos 3$ and $\sin 3$

• A) \[\begin{array} { | c | c | c | } \hline & \text { Approximate } & \text { Calculator } \\ \hline \cos 3 & 0.9 < \cos 3 < 1 & 0.99 \\ \hline \sin 3 & - 0.2 < \sin 3 < - 0.1 & - 0.14 \\ \hline \end{array}\]
• B) \[\begin{array} { | c | c | c | } \hline & \text { Approximate } & \text { Calculator } \\ \hline \cos 3 & 0.1 < \cos 3 < 0.2 & 0.14 \\ \hline \sin 3 & - 1 < \sin 3 < - 0.9 & - 0.99 \\ \hline \end{array}\]
• C) \[\begin{array} { | c | c | c | } \hline & \text { Approximate } & \text { Calculator } \\ \hline \cos 3 & 0.9 < \cos 3 < 1 & 0.99 \\ \hline \sin 3 & 0.1 < \sin 3 < 0.2 & 0.14 \\ \hline \end{array}\]
• D) \[\begin{array} { | c | c | c | } \hline & \text { Approximate } & \text { Calculator } \\ \hline \cos 3 & - 0.2 < \cos 3 < - 0.1 & - 0.14 \\ \hline \sin 3 & 0.9 < \sin 3 < 1 & 0.99 \\ \hline \end{array}\]
• E) \[\begin{array} { | c | c | c | } \hline & \text { Approximate } & \text { Calculator } \\ \hline \cos 3 & - 1 < \cos 3 < - 0.9 & - 0.99 \\ \hline \sin 3 & 0.1 < \sin 3 < 0.2 & 0.14 \\ \hline \end{array}\]

---

Definitions:

Concrete Situations

Circumstances or conditions that are specific, real, and tangible, as opposed to abstract or theoretical scenarios.

Reason Logically

The cognitive process of applying logical thinking and deduction to form valid conclusions or solve problems.

Jean Piaget

A Swiss psychologist known for his pioneering work in child development and his theory of cognitive development.

Informal Assessment Procedures

Informal assessment procedures are non-standardized methods of evaluating a student's performance, such as observations, interviews, and portfolio assessments, to guide instruction.