A Triangle Is Inscribed in a Semicircle of Diameter 6R $\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$

question 18

Multiple Choice

A triangle is inscribed in a semicircle of diameter 6R. Show that the smallest possible value for the area of the shaded region is 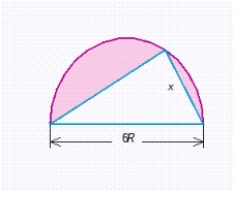$\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }$ . Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.

• A) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to \(A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }\) . The square of the area of the triangle is equal to \(( A ( x ) ) ^ { 2 } = 9 R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }\) , and the substitution \(x ^ { 2 } = t\) will transform this expression into the quadratic function \(- \frac { 1 } { 4 } t ^ { 2 } + 9 R ^ { 2 } t ( 1 )\) Since we want to find the maximum value of t, we will substitute the value \(t = 18 R ^ { 2 } = x ^ { 2 }\) into the equation. Solving for t gives us the following minimum area of the shaded region: \(t = \frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }\) .
• B) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to \(A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }\) . The square of the area of the triangle is equal to \(( A ( x ) ) ^ { 2 } = 9 R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }\) The substitution \(x ^ { 2 } = t\) will transform this expression into the quadratic function \(- \frac { 1 } { 4 } t ^ { 2 } + 9 R ^ { 2 } t ( 1 )\) Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is \(t = \frac { - b } { 2 a } = 18 R ^ { 2 }\) Substituting the value \(t = 18 R ^ { 2 }\) into the equation \(t = x ^ { 2 }\) gives us \(x ^ { 2 } = 18 R ^ { 2 }\) and consequently \(x = 3 R \sqrt { 2 }\) (The negative root can be rejected since the side of a triangle can't be negative). With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to \(\frac { 9 \pi R ^ { 2 } } { 2 } - \frac { 1 } { 2 } x \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }\) Substituting the value \(x = 3 R \sqrt { 2 }\) in the equation (2) gives us that the minimum value of the shaded region is equal to \(\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }\) .
• C) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to \(\frac { 1 } { 4 } 9 R ^ { 2 } x ^ { 2 } + \frac { 1 } { 4 } x ^ { 4 }\) . The substitution \(x ^ { 2 } = t\) will transform this into the quadratic function \(\frac { 1 } { 4 } 9 R ^ { 2 } t + \frac { 1 } { 4 } t ^ { 2 }\) Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is \(t = \frac { - b } { 2 a } = 9 R ^ { 2 }\) Substituting the value \(t = 9 R ^ { 2 }\) into the equation \(t = x ^ { 2 }\) gives us \(x ^ { 2 } = 9 R ^ { 2 }\) and consequently \(x = 3 R\) . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to \(\pi 9 R ^ { 2 } - \frac { 1 } { 2 } x \sqrt { 6 R ^ { 2 } - x ^ { 2 } }\) Substituting the value \(x = 3 R\) into the equation (2), we find that the minimum value of the shaded region is equal to \(\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }\) .
• D) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to \(A ( x ) = \frac { x } { 2 } \sqrt { ( 6 R ) ^ { 2 } - x ^ { 2 } }\) , which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as: \(x ^ { 2 } = \frac { - b } { 2 a } = 18 R ^ { 2 }\) We can then write \(x ^ { 2 } = 18 R ^ { 2 }\) as \(x ^ { 2 } = 18 R ^ { 2 }\) and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area: \(\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }\) .
• E) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to \(\frac { 1 } { 2 } 9 ^ { 2 } R ^ { 2 } x ^ { 2 } - \frac { 1 } { 4 } x ^ { 4 }\) . The substitution \(x ^ { 2 } = t\) will transform this into the quadratic function \(\frac { 1 } { 2 } 9 ^ { 2 } R ^ { 2 } t - \frac { 1 } { 4 } t ^ { 2 }\) Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is \(t = \frac { - b } { 2 a } = 3 R ^ { 2 }\) Substituting the value \(t = 3 R ^ { 2 }\) into the equation \(t = x ^ { 2 }\) gives us \(x ^ { 2 } = 3 R ^ { 2 }\) and consequently \(x = R \sqrt { 7 }\) . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to \(\frac { \pi 9 R ^ { 2 } } { 4 } - \frac { 1 } { 2 } x \sqrt { 9 R ^ { 2 } - x ^ { 2 } }\) Substituting the value \(x = R \sqrt { 7 }\) into the equation (2), we find that the minimum value of the shaded region is equal to \(\frac { 9 ( \pi - 2 ) R ^ { 2 } } { 2 }\) .

---

Definitions:

Binding Precedent

A binding precedent refers to a legal case decision that must be followed by lower courts within the same jurisdiction in future cases with similar circumstances.

Stare Decisis

The legal principle of determining points in litigation according to precedent, which means to stand by things decided in previous judicial decisions.

Administrative Agencies

Governmental bodies with the authority to implement and administer particular legislation, often involved in the detailed regulation of various aspects of government policy.

Federal Administrative Agencies

Bodies established by the federal government of a country to implement and administer particular legislation and regulations.