The Area of a Circle with Radius 1 Is π $\sqrt { 1 - x ^ { 2 } }$

question 52

True/False

The area of a circle with radius 1 is π. If f(x) = $\sqrt { 1 - x ^ { 2 } }$ gives the top half of this circle, as illustrated below, use the second Taylor polynomial of f(x) at x = 0 to find an approximate value for π. Is the following correct? 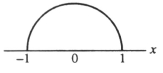$$\begin{array} { l } \mathrm { p } 2 ( \mathrm { x } ) = 1 - \frac { 1 } { 2 } \mathrm { x } ^ { 2 } \\\frac { \pi } { 2 } \approx \int _ { - 1 } ^ { 1 } \left( 1 - \frac { 1 } { 2 } \mathrm { x } ^ { 2 } \right) \mathrm { dx } = \frac { 5 } { 3 } \text { so } \pi \approx \frac { 10 } { 3 }\end{array}$$

---

Definitions:

Clients

Individuals or entities that seek and receive professional services or advice from a business or professional individual in return for payment.

Clique Formations

The process by which groups of individuals with similar interests, values, or backgrounds form exclusive groups within a larger community.

Rivalries

Competitive or antagonistic interactions or relationships between individuals, groups, or entities.