Use the figure to answer the question.
The figure represents the parabolic trajectory of a ball going from a to e in Earth gravity but without air resistance. The initial velocity of the ball is Vo at an angle 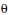 to the horizon. The vertical dashed lines represent equal time interval,
to the horizon. The vertical dashed lines represent equal time interval, 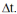

-The vertical velocity at point b is: Note: (g = 9.81 m/s2)
Definitions:
Q14: A motorcycle of mass m starting from
Q17: The torque exerted on a perfectly spherical
Q21: Which of the following involves differentiation among
Q26: An example of a philanthropic organization is:<br>A)
Q29: An example of a macroeconomics issue faced
Q33: A person's skin color is an example
Q33: One of the greatest health concerns is
Q34: A 35-year-old man from Russia comes to
Q44: You are whirling a stone on the
Q90: A block that has a mass M