Examlex

Solved

Two Curves Are Said to Be Orthogonal If Their Tangent

question 120

Essay

Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
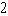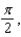y - Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal. y - x = x = cos y x = Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal. y - x = x = cos y x = Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal. y - x = x = 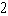cos y cos y Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal. y - x = x = cos y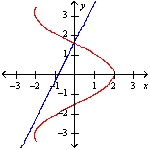

Definitions:

Bismarck's Policy

The political strategies and foreign policies implemented by Otto von Bismarck, Chancellor of the German Empire, aimed at achieving German unification and maintaining European stability through diplomacy and the balance of power.

Catholicism

The branch of Christianity headed by the Pope, based in Rome, and characterized by its traditions, teachings, and practices.

German Emperor

The title used for the monarch and head of state of Germany, particularly associated with the rulers of the German Empire from 1871 to 1918.

William II

William II, also known as Wilhelm II, was the last German Emperor (Kaiser) and King of Prussia, ruling from 1888 until his abdication in 1918.

Related Questions

Q4: For what values of a and b

Q36: Classify the function as a Rational function,

Q51: Guttery Corporation has provided the following financial

Q63: Express the sum as a single integral

Q65: Define the function <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Define the

Q84: Find the points of intersection of the

Q96: Sketch the graph of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5971/.jpg" alt="Sketch

Q97: What is the shortest possible length of

Q111: Zack Company has a current ratio of

Q138: Find a third-degree polynomial Q such that