The Figure Shows a Pendulum with Length L and the Angle

question 3

Multiple Choice

The figure shows a pendulum with length L and the angle $\theta$ from the vertical to the pendulum. It can be shown that $\theta$ , as a function of time, satisfies the nonlinear differential equation $\frac { d ^ { 2 } \theta } { d t ^ { 2 } } + \frac { g } { L } \sin \theta = 0$ where $g = 9.8 \mathrm {~m} / \mathrm { s } ^ { 2 }$ $\text { is the acceleration due to gravity. For small values of }$ $\theta$ we can use the linear approximation 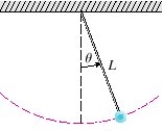$\sin \theta = \theta$ $\text { and then the differential equation becomes linear. Find the equation }$ $\text { of motion of a pendulum with length } 1 \mathrm {~m} \text { if } \theta \text { is initially } 0.2 \mathrm { rad } \text { and the initial }$ $\text { angular velocity is }$ $\frac { d \theta } { d t } = 1 \mathrm { rad } / \mathrm { s }$

• A) \[\theta ( t ) = 0.2 \cos ( \sqrt { 9.8 } t ) + \frac { 1 } { \sqrt { 9.8 } } \sin ( \sqrt { 9.8 } t )\]
• B) \(\theta ( t ) = 0.2 \cos ( \sqrt { 9.8 } t ) + 2 \sin ( \sqrt { 9.8 } t )\)
• C) \(\theta ( t ) = 2 \cos ( 9.8 t ) + \frac { 1 } { 9.8 } \sin ( 9.8 t )\)
• D) \(\theta ( t ) = \frac { 1 } { 9.8 } \cos ( \sqrt { 9.8 } t ) + 0.2 \sin ( \sqrt { 9.8 } t )\)
• E) \(\theta ( t ) = 0.2 \sin ( \sqrt { 9.8 } t ) + \frac { 1 } { \sqrt { 9.8 } } \cos ( \sqrt { 9.8 } t )\)

---

Definitions:

Set Point

Set point refers to the theory suggesting that the body regulates its weight and other physiological functions around a predetermined, stable value or range.

Basal Metabolic Rate

The speed at which the body consumes energy when at rest in order to sustain essential operations like breathing and maintaining body temperature.

Feelings of Hunger

The physiological and psychological sensation that prompts an individual to seek and consume food.

Set Point

A theory suggesting that the body regulates its weight around a genetically predetermined 'set point.'