The Figure Shows a Pendulum with Length L and the Angle

question 3

Multiple Choice

The figure shows a pendulum with length L and the angle $\theta$ from the vertical to the pendulum. It can be shown that $\theta$ , as a function of time, satisfies the nonlinear differential equation $\frac { d ^ { 2 } \theta } { d t ^ { 2 } } + \frac { g } { L } \sin \theta = 0$ where $g = 9.8 \mathrm {~m} / \mathrm { s } ^ { 2 }$ $\text { is the acceleration due to gravity. For small values of }$ $\theta$ we can use the linear approximation 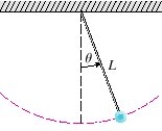$\sin \theta = \theta$ $\text { and then the differential equation becomes linear. Find the equation }$ $\text { of motion of a pendulum with length } 1 \mathrm {~m} \text { if } \theta \text { is initially } 0.2 \mathrm { rad } \text { and the initial }$ $\text { angular velocity is }$ $\frac { d \theta } { d t } = 1 \mathrm { rad } / \mathrm { s }$

• A) \[\theta ( t ) = 0.2 \cos ( \sqrt { 9.8 } t ) + \frac { 1 } { \sqrt { 9.8 } } \sin ( \sqrt { 9.8 } t )\]
• B) \(\theta ( t ) = 0.2 \cos ( \sqrt { 9.8 } t ) + 2 \sin ( \sqrt { 9.8 } t )\)
• C) \(\theta ( t ) = 2 \cos ( 9.8 t ) + \frac { 1 } { 9.8 } \sin ( 9.8 t )\)
• D) \(\theta ( t ) = \frac { 1 } { 9.8 } \cos ( \sqrt { 9.8 } t ) + 0.2 \sin ( \sqrt { 9.8 } t )\)
• E) \(\theta ( t ) = 0.2 \sin ( \sqrt { 9.8 } t ) + \frac { 1 } { \sqrt { 9.8 } } \cos ( \sqrt { 9.8 } t )\)

---

Definitions:

Zero-Coupon Bond

Is a debt security that doesn't pay interest (a coupon) but is traded at a deep discount, providing profit at maturity when the bond is redeemed for its full face value.

Rate Of Return

The gain or loss on an investment over a specified time period, expressed as a percentage of the investment’s cost.

Break-Even Interest Rate

The interest rate at which an investment generates returns that are sufficient to cover the costs associated with the investment, resulting in a net profit of zero.

Zero-Coupon Bond

A bond that does not pay interest during its life but is sold at a discount and pays its full face value at maturity.