Two Curves Are Said to Be Orthogonal If Their Tangent $\frac{3}{4}$

question 41

Short Answer

Two curves are said to be orthogonal if their tangent lines are perpendicular at each point of intersection of the curves. Show that the curves of the given equations are orthogonal.
y - $\frac{3}{4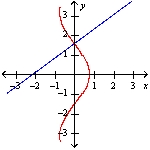}$ x = $\frac{\pi}{2}$ x = $\frac{3}{4}$ cos y

---

Definitions:

Flexibility

The quality of being adaptable or variable, especially the ability to respond to changes in circumstances or environments.

Productivity

The measure of efficiency in converting inputs into useful outputs, commonly used in analyzing the performance of businesses, economies, or individual workers.

Supervisory Costs

Expenses associated with overseeing and managing employees, including salaries of supervisors and costs related to training and supervising staff.

Flexible Benefit Plans

Employee benefit programs that allow workers to choose from a variety of pre-tax benefits, tailoring the package to their personal needs.