Bernoulli's equation for nonviscous flow can be stated as
P1 + gy1 + 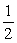 v12 = P2 + gy2 +
v12 = P2 + gy2 +  v22
v22
A fluid is flowing through a horizontal tube that changes in cross-sectional area from
A1= 0.75 cm2 to A2 = 0.030 cm2.  When v1 = 3.5 cm/s, = 1.4 g/cm3, and viscosity is neglected, the difference between pressure P2 at A2 and P1 at A1 is
When v1 = 3.5 cm/s, = 1.4 g/cm3, and viscosity is neglected, the difference between pressure P2 at A2 and P1 at A1 is
Definitions:
Customs Brokers
Professionals who assist businesses in navigating the complexities of customs regulations to import and export goods.
Non Vessel-owning Common Carriers
Third-party companies that provide shipment forwarding services without owning the vessels used for transportation, typically organizing logistics for shipping goods.
Near-shoring
The practice of transferring a business operation or service to a nearby country, rather than a far-off location, to reduce costs and improve communication and control.
On-shoring
The practice of bringing business operations back to the company's country of origin from overseas to improve control and reduce costs.
Q6: The figure shows a standing wave in
Q17: Two monoatomic gases, helium and neon,
Q28: What must be the length of a
Q34: A gas has a density X at
Q65: A wheel is rotating at 30
Q70: Pressure as a function of depth for
Q73: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6080/.jpg" alt=" Two identical bodies
Q82: At what depth in sea water
Q85: According to Newton's law of universal gravitation,
Q106: You have a friend who lives in