Suppose a Population of Bacteria Is Changing at a Rate

qu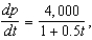estion 14

Multiple Choice

Suppose a population of bacteria is changing at a rate of where t is the time in days. The initial population (when t = 0) is 1,500. Identify an equation that gives the population at any time t and use it to find the population when 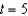days. Round your answer to the nearest integer.

• A) 12,783
• B) 11,525
• C) 13,533
• D) 10,772
• E) 11,522

Appreciate the importance of studying human development across the lifespan and recognize the nine periods of development.

Understand the role and functions of Institutional Review Boards (IRBs) in psychological research.

Analyze a developmental issue from a visual perspective and differentiate it from similar perspectives.

Understand the concepts of reliability and validity in research and their importance for scientific inquiry.

---

Definitions:

Order Cycle Time

The total time taken from when a customer places an order until the product is delivered to them.

Physical Distribution

The activities involved in moving a product from the manufacturer to the consumer, including warehousing, transportation, and inventory management.

Total Logistics Cycle

The comprehensive process that includes planning, implementing, and controlling the efficient flow and storage of goods, services, and related information from point of origin to point of consumption.

Replenishment Time

The duration required to restock or refill inventory to its desired level after it has been depleted.