Use the following steps.
A) Write an equation for the areas using integrals.
B) Differentiate the equation in A and solve the resulting linear equation.
Ans:
A) 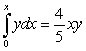 B)
B) 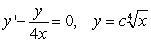
-A pool contains 12 million gal of fresh water. Contaminated water flows into the pool at a rate of 4 million gal/year as the mixture in the pool flows out at the same rate.
The concentration 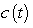 of the chemical in the incoming contaminated water is
of the chemical in the incoming contaminated water is  g/gal, where t is in years.
g/gal, where t is in years.
Find the amount 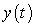 of the chemical in the pool at time
of the chemical in the pool at time 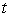 .
.
Definitions:
Q4: Find the speed and the length of
Q14: Use the Comparison Tests to determine if
Q15: Compute the area of the surface obtained
Q20: Find the length of the polar curve
Q27: Consider the 3 lines. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Consider
Q35: A cereal-packaging company fills boxes on average
Q44: A vertical tank, with elliptic horizontal cross
Q49: The face of a dam is an
Q80: The two lines <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The two
Q93: The decomposition <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The decomposition