The Height of Sixth Grade Students in a Class Is

question 40

Essay

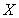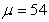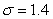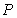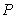The height of sixth grade students in a class is a random variable with mean in. Assume the height of the students is normally distributed with standard deviation in. Let be the probability that a student will be at most in. tall. Express as an integral of an appropriate density function, and compute its value numerically.

---

Definitions:

Accord and Satisfaction

Accord and satisfaction is a legal contract where a dispute is settled by the parties involved agreeing to give and accept something of value in different terms than the original agreement.

UCC Section 3-311

A provision in the Uniform Commercial Code that addresses the accord and satisfaction by use of a negotiable instrument.

Paid-in-Full Check

A paid-in-full check is a check by which the issuer intends to settle a debt completely, often accompanied by a statement indicating that the payment is meant to resolve the obligation in full.

Different Performance

Fulfillment of contractual obligations in a manner that is different from what was specifically agreed upon, sometimes acceptable with mutual consent.