The Height of Sixth Grade Students in a Class Is

question 40

Essay

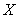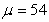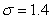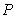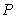The height of sixth grade students in a class is a random variable with mean in. Assume the height of the students is normally distributed with standard deviation in. Let be the probability that a student will be at most in. tall. Express as an integral of an appropriate density function, and compute its value numerically.

---

Definitions:

Double-Declining-Balance

A method that determines a depreciation amount for the first year that is approximately twice the straight-line rate.

Scrap Value

The predicted revenue from selling an asset at the conclusion of its serviceable life.

Units-Of-Production Method

A depreciation method that allocates cost based on the actual usage, activity, or units of production of the asset.

Scrap Value

The estimated resale value of an asset at the end of its useful life, often considered in depreciation calculations.