Examlex

Solved

If and Then Does Not Converge to a Finite

question 76

Multiple Choice

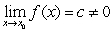If If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 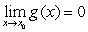and If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 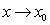then If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. 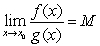does not converge to a finite limit as If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
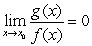For proving, we assume that If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. exists and is finite. Then
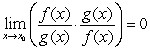By the Quotient Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. and by the Product Rule If and then does not converge to a finite limit as . For proving, we assume that exists and is finite. Then By the Quotient Rule and by the Product Rule . Which of the statements below completes the proof? A) From , it follows that 1=0, which is a contradiction. B) From , we can conclude that , which contradicts our assumption. C) From , we can conclude that , which contradicts our assumption. D) From , we can conclude that , which contradicts our assumption. E) A and C are correct. .
Which of the statements below completes the proof?

Definitions:

Carrying Value

The book value of assets and liabilities on a company’s balance sheet, often different from the market value.

Discount On Bonds

The difference between the face value of a bond and its selling price, when the bond is sold for less than its face value.

Premium

The amount paid in excess of a standard cost or the face value of a financial instrument, often associated with insurance policies, bonds, and options.

Carrying Value

The book value of assets and liabilities as represented in the financial statements, excluding the market value.

Related Questions

Q2: Which statement is true about the estimated

Q3: Find the interval over which the function

Q3: Determine the points where the function is

Q9: Let <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Let denote

Q13: At α = 0.05,<br>A) we reject the

Q14: Which of the following statements is true

Q29: By Newton's Law of Cooling, an object

Q33: A least squares estimated regression line has

Q41: The derivative of <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="The derivative

Q71: Show that the equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB5596/.jpg" alt="Show